whosbug项目中,最重要的无非是两个部分:
whosbug初版发布后我们进行了一系列的测试,发现了老算法在一些场景下的局限性(如对没有第三方库调用的处理、多语言下的泛用性不足等问题)
于是在参考了部分论文后,我们结合实际落地场景设计了新的责任人归属算法 —— Keyman ,本文我们就详细介绍下算法设计
为了清晰一个函数在语法树中的精确位置,首先我们需要每个函数的唯一标识,这里我们的标识为:
并且包 / 类也视作一个函数,将包/类内的代码非函数内代码归入这个包 / 类的函数
Init: 获取预设的迭代次数NUMBER_OF_ITERATION,新建相关方法集methods,以错误堆栈中涉及的所有方法为初值不断地从methods内的每个函数/方法找到与其相连且未在methods内的方法,加入methods中,也同时得到该方法与直接错误方法的距离。如此全面进行NUMBER_OF_ITERATION次 1 2 3 4 5 6 7 8 9 10 11 NUMBER_OF_ITERATION = 3 methods = stacks.all_methods() for i in range (NUMBER_OF_ITERATION): for method in methods: members = ['father' , 'son' , 'brother' ] for member in members: method_got = method.__getattribute__(member) if method_got not in methods: method_got.relevance_weight = method.relevance_weight + 1 methods.append(method_got)
考虑一个函数与直接导致错误的函数(输入的堆栈中的原始栈帧)的距离(语法树中的距离)、其原始栈帧到栈顶的距离以及其置信度
C o n t r i b u t i o n = C o n f i d e n c e ∗ 1 f r a m e N u m b e r + 1 ∗ ( N U M B E R _ O F _ I T E R A T I O N − r e l e v a n c e D i s t ) \mathit{Contribution}\ =\ \mathit{Confidence\ *\ \frac{1}{frameNumber+1}\ *\ \left( NUMBER\_OF\_ITERATION - relevanceDist \right)} C o n t r i b u t i o n = C o n f i d e n c e ∗ f r a m e N u m b e r + 1 1 ∗ ( N U M B E R _ O F _ I T E R A T I O N − r e l e v a n c e D i s t )
置信度的设定能保证:
函数保留的越久越可信(时间维度 上的考虑,一定程度上也考虑了初版的假设:越近的修改越容易导致bug) 函数大改时会基本回落到初始化的置信度 一定程度上区分bugfix型的变动和业务 变更的变动 C o n f i d e n c e = a l i n e C o u n t ∗ S u b M e t h o d . C o n f i d e n c e ‾ ( a ϵ ( 0 , 1 ) ) \mathit{Confidence\ =\ a^{lineCount}\ *\ \overline{SubMethod.Confidence} \quad \left(a\ \epsilon (0,1)\right)} C o n f i d e n c e = a l i n e C o u n t ∗ S u b M e t h o d . C o n f i d e n c e ( a ϵ ( 0 , 1 ) )
以下两种情况下,S u b M e t h o d . C o n f i d e n c e SubMethod.Confidence S u b M e t h o d . C o n f i d e n c e
一个函数没有调用子函数时,S u b M e t h o d . C o n f i d e n c e ‾ \overline{SubMethod.Confidence} S u b M e t h o d . C o n f i d e n c e 调用的子函数为系统函数 / 第三方库函数时,S u b M e t h o d . C o n f i d e n c e SubMethod.Confidence S u b M e t h o d . C o n f i d e n c e C o n f i d e n c e : = ( r e m a i n L i n e C o u n t l i n e C o u n t ∗ o l d C o n f i d e n c e + n e w L i n e C o u n t l i n e C o u n t ∗ a n e w L i n e C o u n t ∗ n e w S u b M e t h o d . C o n f i d e n c e ‾ ) P r o p e n s i s t y F o r C h a n g e \mathit{Confidence := \left(\frac{remainLineCount}{lineCount}\ *oldConfidence\ + \frac{newLineCount}{lineCount}*a^{newLineCount}\ *\overline{newSubMethod.Confidence}\right)^{PropensistyForChange}} C o n f i d e n c e : = ( l i n e C o u n t r e m a i n L i n e C o u n t ∗ o l d C o n f i d e n c e + l i n e C o u n t n e w L i n e C o u n t ∗ a n e w L i n e C o u n t ∗ n e w S u b M e t h o d . C o n f i d e n c e ) P r o p e n s i s t y F o r C h a n g e
函数大改时,r e m a i n L i n e C o u n t l i n e C o u n t ∗ o l d C o n f i d e n c e \frac{remainLineCount}{lineCount}\ *oldConfidence l i n e C o u n t r e m a i n L i n e C o u n t ∗ o l d C o n f i d e n c e
变更倾向系数基于以下假设,在一个函数的一次变更内:
逻辑代码行的修改越多,我们越倾向于认为这是一次bugfix 调用方法行的修改越多,我们越倾向于认为这是一次业务更新 代码留存的时间越长,认为其置信度越高 P r o p e n s i s t y F o r C h a n g e = t r a n s ( Δ l o g i c L i n e C o u n t / l o g i c L i n e C o u n t Δ f u n c t i o n C a l l C o u n t / f u n c t i o n C a l l C o u n t + d ) t r a n s ( x ) = b c x b ϵ ( 0 , 1 ) , c ϵ ( 0 , + ∞ ) , d ϵ ( 0 , + ∞ ) P r o p e n s i s t y F o r C h a n g e ϵ ( 0 , b c d ] \mathit{PropensistyForChange\ =\ trans\left(\frac{\Delta{logicLineCount/logicLineCount}}{\Delta{functionCallCount}/functionCallCount}+d\right)} \\ \mathit{trans(x)\ =\ b^{cx}} \\ b\ \epsilon\ (0\ ,\ 1),\ c\ \epsilon\ (0\ ,+\infty),\ d\ \epsilon\ (0\ ,+\infty)\\ \mathit{PropensistyForChange}\ \epsilon \left(0,b^{cd}\right] P r o p e n s i s t y F o r C h a n g e = t r a n s ( Δ f u n c t i o n C a l l C o u n t / f u n c t i o n C a l l C o u n t Δ l o g i c L i n e C o u n t / l o g i c L i n e C o u n t + d ) t r a n s ( x ) = b c x b ϵ ( 0 , 1 ) , c ϵ ( 0 , + ∞ ) , d ϵ ( 0 , + ∞ ) P r o p e n s i s t y F o r C h a n g e ϵ ( 0 , b c d ]
trans函数用于值域变换,使变更倾向归一化到( 0 , b c d ] \left(0,b^{cd}\right] ( 0 , b c d ] b, c对曲线的走向有一定影响
同时超参数d使得PropensistyForChange始终小于1,保证每次置信度更新时都会更趋近于1(代码留存的时间越长,认为其置信度越高)
1 2 3 4 5 6 7 8 9 10 commiters = [] contribution_rate = 1 for commit in related_commits: weight = commit.commiter.weight weight += contribution_rate*(changed_line_count/all_line_count)*Confidence commiters.append(commit.commiter) unchanged_rate *= 1 -(changed_line_count/all_line_count) commiters.sortByWeight(reverse = True )
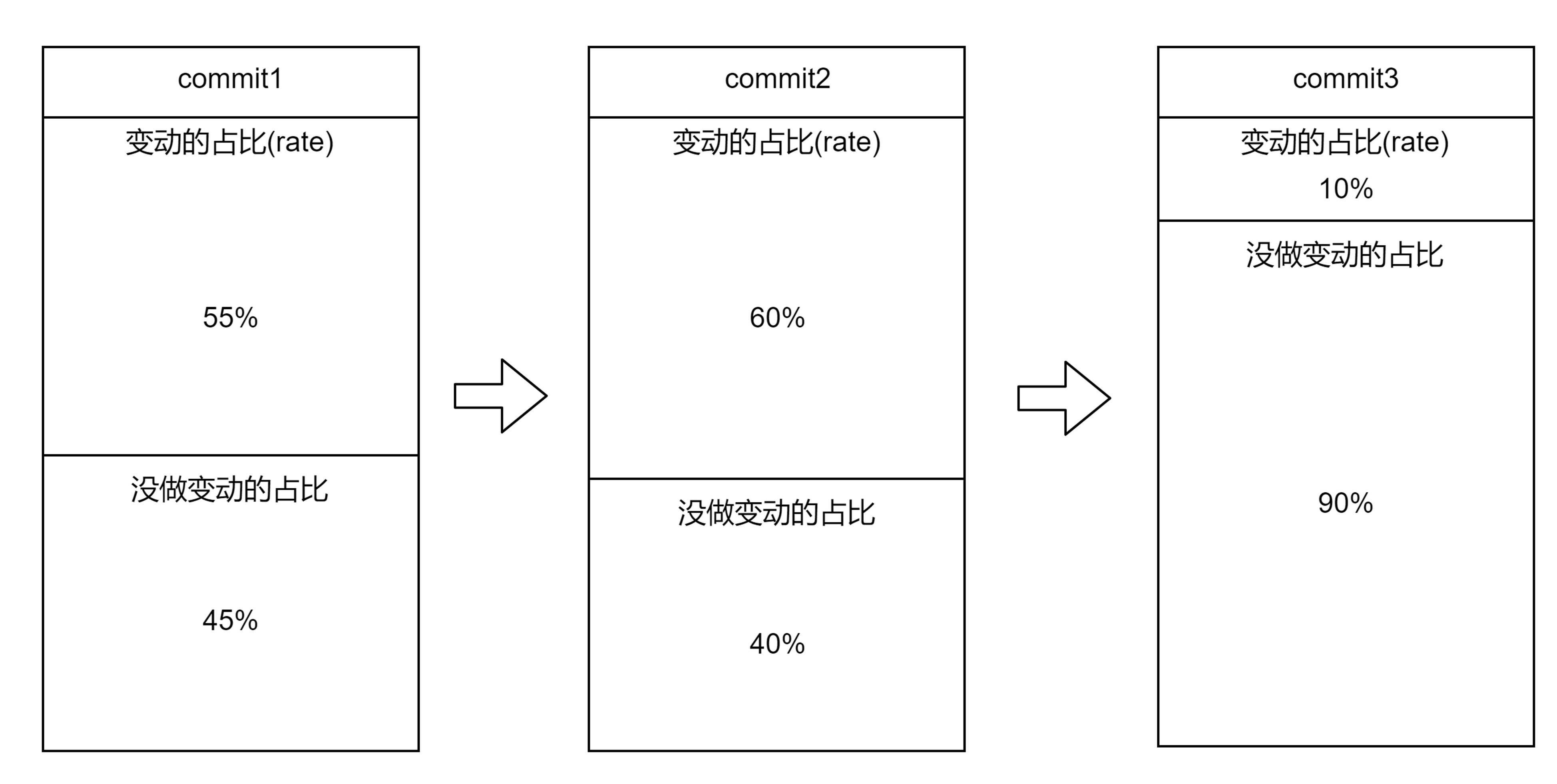
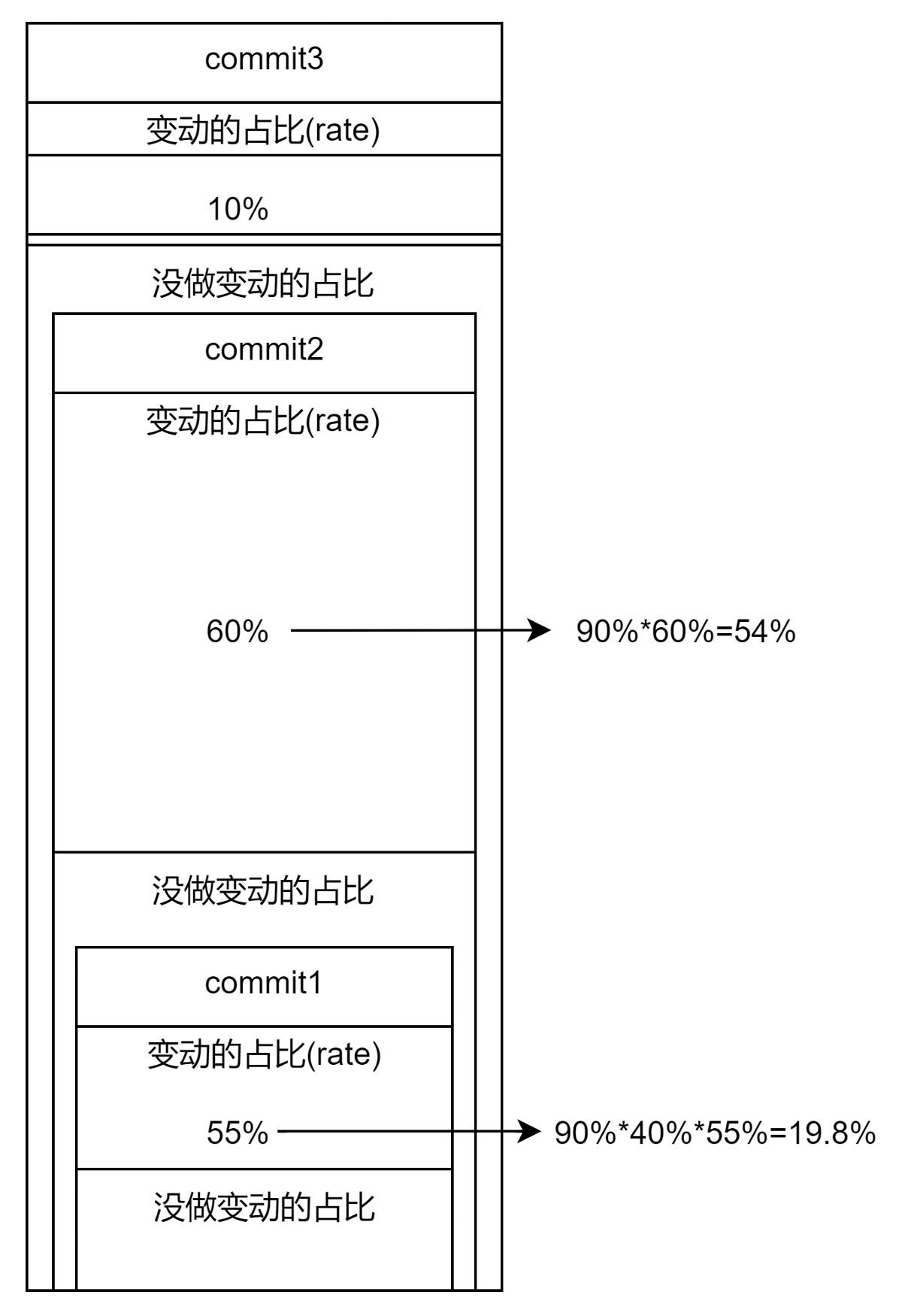
假设:有三次不同的commit存在,且三次提交的变动情况如图,
会被处理为